Research Topics
Research Topics
Argumentation is one of the major fields in Artificial Intelligence (AI). Numerous applications in diverse domains like legal reasoning, multi-agent systems, social networks, e-government, decision support and many more make this topic very interdisciplinary and lead to a wide range of different formalizations. Out of them the concept of abstract Argumentation Frameworks (AFs) is one of the most popular approaches to capture certain aspects of argumentation. This very simple yet expressive model has been introduced by Phan Minh Dung in 1995. Arguments and a binary attack relation between them, denoting conflicts, are the only components one needs for the representation of a wide range of problems and the reasoning therein. Nowadays numerous semantics exist to solve the inherent conflicts between the arguments by selecting sets of “acceptable” arguments. Depending on the application, acceptability is defined in different ways.
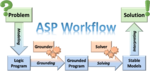
Answer Set Programming (ASP) is a modern approach towards true declarative programming (and declarative problem solving). Based on non monotonic reasoning, it represents an important logic-programming paradigm. Any program consists of (logical) rules, which describe the problem of interest. Programs are then evaluated under the answer-set semantics (or stable model semantics), such that each of the program's answer sets is a solution. Therefore, one is focused on describing some problem by the means of specifying appropriate rules, rather than bothering about how to solve the problem.
We are mainly interested in using ASP as efficient computational approach to tackle problems of our other research areas, for example, we compute different semantics of Argumentation Frameworks using an ASP based system ASPARTIX.
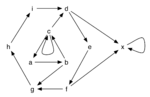
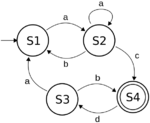
Automata theory is concerned with the study of abstract machines, their computations and computational problems. In essence, automata can be understood as finite representations of (potentially) infinite formal languages, and they vary in their expressive power depending on their specific design.
Finite-state automata, recognizing the regular languages, are one of the most fundamental formalisms in theoretical computer science and have proven to be a useful tool in many areas, such as compiler construction, formal verification, or as a means of proving the decidability of expressive logics applied to knowledge representation.
Especially in the areas mentioned, it is desirable to model situations that go beyond regularity. In this research project, we are interested in (tree) automata models that are enriched by counting mechanisms.
Database theory deals with a broad range of topics related to data management and data management systems. Its theoretical foundations stem from logic, most notably relational algebra, and first-order logic. It focuses, among other subjects, on the computational complexity and the expressive power of query languages. Traditionally, database theory has studied the relational model - where databases and queries can be viewed as relational structures and query evaluation boils down to finding an appropriate homomorphism between two structures. However, in recent years, one can see a steady rise of other models. The most notable example is the graph model, where structures are restricted to binary signatures and queries are lifted to regular expressions.
Description Logics represent one of today's major paradigms in Knowledge Representation. They have developed out of semantic networks and frame-based approaches.
Existential Rules are a knowledge representation formalism used in artificial intelligence and database theory. Their syntactic flexibility enables an easy integration of both semantic knowledge and databases. Syntactically close to Datalog rules, an important distinguishing feature is the possibility to describe individuals whose existence was not originally known, which is of great help for modeling purposes. All these features have motivated an intense research effort on how to query data under such rules. Questions typically tackled with this respect are the following: which query language achieve a good tradeoff between expressivity and complexity? What ensures the decidability of the query answering problem? What is the complexity of specific classes of rules? How to build efficient reasoners?
Formal Concept Analysis is a mathematical theory which describes concepts and conceptual hierarchies by means of lattice theory. Thereby, the basis are formal contexts, elementary data structures that describe objects and their attributes. A formal concept is then composed of a set of objects and a set of attributes which -- in line with philosophical and linguistic traditions -- are called concept extent and concept intent, respectively. Formal concepts can then be put into relation to each other, forming a hierarchy of sub- and superconcepts. Formal Concept Analysis was founded in the 1980s in Darmstadt in the group of Rudolf Wille and has become a discipline with numerous practical applications in diverse areas, including data- and textmining, knowledge management, Semantic Web, software engineering, economics or biology.
Knowledge representation and reasoning (KRR) is concerned with the encoding of human knowledge in computer systems such that it can serve as a basis for drawing logical conclusions. By means of logical reasoning, KRR systems derive implicit knowledge from the given information. KRR plays an important role in constructing more intelligent computer systems, but it is also used in applications where large knowledge bases need to be constructed, since reasoning can help to reduce redundancy and to detect errors.
Most modern KRR approaches are based on formal logics, with description logics and rule-based formalisms constituting the most prominent language families. In applied fields, knowledge bases are used to construct ontologies, which relates KRR to other research topics, such as semantic technologies. While KRR is based on a large body of theoretical research, it also includes many applied topics, such as the design and implementation of tools for automated reasoning.
Modal and temporal logics are logical formalisms with possible world semantics, used for reasoning about a variety of phenomena such as the behaviour of programs, software systems, ethical norms, knowledge, and agential action. Canonical examples involve the basic modal logic K, linear-time temporal logic LTL, branching-time logics like CTL or CTL*, dynamic epistemic logic, and STIT logics.
The research includes establishing the precise complexity of standard reasoning problems as well as designing efficient proof systems.
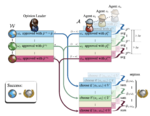
Multi-agent systems (MAS) focus on the interaction of autonomous agents—entities capable of independent decision-making—situated in a shared environment. MAS research investigates how agents can cooperate, compete, or coordinate their actions to achieve individual or collective goals. The theoretical foundations of this field draw from game theory, social choice, distributed computing, and artificial intelligence more broadly. A key concern in MAS is the design of mechanisms that enable efficient collaboration or competition among agents, particularly when they act based on clear objectives. In our research, we often assume that agents are presented with a set of possible choices. While all the agents are aware of these choices, they do not know which option represents the correct or superior choice—the ground truth. In such systems, the agents collaborate with the objective of identifying this ground truth, which remains unknown to them at the outset.
Natural Language Understanding (NLU) is a broad area of research that addresses the problem of interpreting and modeling the semantics and pragmatics of natural language, using a diverse set of techniques for this purpose. Since human reasoning is often mediated by natural language, success in this area is key for intelligent systems to successfully support human reasoning.
Themes in our range of interest include the representation and reasoning with human-like concepts, with incomplete, uncertain or vague statements and with pragmatic or non-explicit information. The methods we use for investigation are mostly based on (but not restricted to) logical frameworks.
Entailment in classical logics (e.g. first-order predicate logic) is montone, that is, if a formula F follows from a set S of formulas, then F also follows from any superset of S.
Non-monotonic reasoning is concerned with entailment relations that do not satisfy monotonicity. Such relations can be used to model default assumptions (such as “delivery is free of charge unless stated otherwise”), rules with exceptions (e.g. “birds typically fly, but penguins do not fly”) or priorities between rules (e.g. federal law trumping state law).
The research area investigates the formal modelling of various approaches to non-monotonic reasoning, analyses and compares such entailment relations and also deals with implementations and applications, e.g. in knowledge representation, logic programming, legal reasoning, or Natural-Language Understanding.
Proof theory serves as one of the central pillars of mathematical logic and concerns the study and application of formal mathematical proofs. Typically, proofs are defined as syntactic objects inductively constructible through applications of inference rules to a given set of assumptions, axioms, or previously constructed proofs. Since proofs are built by means of inference rules, which manipulate formulae and symbols, proof theory is syntactic in nature, making proof systems well-suited for logical reasoning in a computational environment. As such, proof theory has proven to be an effective tool in automated reasoning, allowing for the design of complexity-optimal decision procedures providing verifiable witnesses for (un)satisfiable logical statements. On the theoretical side, techniques in proof theory can be used to establish the consistency, decidability, or interpolability of logics, among other significant properties.
Common questions that arise in the domain of proof theory are: What constitutes a mathematical proof? How can proof systems be constructed so that they are suitable in automated reasoning? What are the relationships between proofs in differing formalisms? How does one construct a proof system for a logic whereby all proofs are analytic (i.e. all information used in the proof is contained in the conclusion of the proof)?
Rule-based reasoning is the general concept of automatically deriving new knowledge by recursively applying rules on data. These rules can be expressed in different formats and can have different properties: Datalog rules do not support functions nor existentially quantified variables, with Existential Rules existentially quantified variables can be derived, and other formalisms like for example Notation3 Logic allow the introduction of more complex constructs.
Rule-based reasoning can be performed with different strategies. Knowledge can be derived by successively applying all rules on data and derived knowledge (forward-reasoning) or going backwards starting from a goal (backward reasoning). Negation can be handled in different ways: everything what cannott be proven can be considered as wrong (Negation as Failure), but there are also frameworks which handle negation in a more First-Order-Logic kind of way taking different possibilities into account (Answer Set Programming).
These and other aspects like for example the kind of practical problems which can be solved by the different existing approaches and the complexity different features add to the reasoning are the field of our research.
Semantic Technologies are comprise a wide field methods and technologies used to represent, manage, exchange, and process semantic data. At the heart of this are machine-readable formats for representing data and schema information (ontologies). A number of related technology standards have been created by the World Wide Web Consortium (W3C) in the context of its Semantic Web and Web of Data activities. The most prominent of these standards are the RDF Resource Description Language (a graph-based data-representation format), the OWL Web Ontology Language (an ontology language based on Description Logics), and the SPARQL Protocol and RDF Query Language (a data management and query language). However, semantic technologies also comprise other approaches, such as the annotation approach of schema.org, as well as aspects of methodology and infrastructure.
Research in semantic technologies is concerned with a variety of applied questions. The specification and processing of ontologies is closely related to the field of knowledge representation and reasoning while other questions touch upon issues of databases, information extraction, or Web systems. The latter aspect comes to the fore in applications of Linked Open Data, but there are also many important uses of OWL and RDF that have little or nothing to do with the World Wide Web.