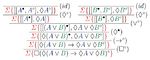Forschungsfelder
Forschungsfelder
Argumentation ist ein wichtiges Forschungsfeld der Künstlichen Intelligenz und des nichtmonotonen Schließens, welches Anwendungen in Bereichen wie z.B. Legal Reasoning, soziale Netzwerke, E-Government, Multi-Agenten-Systeme und Decision Support findet. Dabei hat sich das Konzept der abstrakten Argumentation Frameworks (AFs) zu einem der beliebtesten Ansätze entwickelt. Dieses relativ einfache aber sehr ausdrucksstarke Modell wurde im Jahre 1995 von Phan Minh Dung eingeführt und besteht, kurz gesagt, aus einer Menge von Argumenten und einer binären Attackrelation zwischen den Argumenten, durch die Konflikte ausgedrückt werden. Dabei ist mit "abstrakt" gemeint, dass man nicht die interne Struktur der Argumente betrachtet, sondern nur die Beziehung der Argumente zueinander, die durch die Attacken gegeben ist. Zur Lösung der Konflikte werden unterschiedliche Semantiken herangezogen, die zulässige Mengen von Argumenten auswählen. Abhängig von der jeweiligen Anwendung genügen diese Semantiken unterschiedlichen Anforderungen.
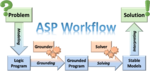
Answer Set Programming (ASP) ist ein Ansatz zur deklarativen Programmierung, basierend auf Logik Programmen evaluiert unter der sogenannten Stable Model Semantik (oder auch Answer Set Semantik). Ein Answer Set ist ein Modell (im Sinne einer Interpretation) des Logik Programms, und repräsentiert eine Lösung des modellierten Problems. Die deklarative Beschreibung (Modellierung) eines Problems steht dabei im Vordergrund, und nicht etwa die algorithmische Herangehensweise um das Problem zu lösen. ASP eignet sich speziell für (Such-)probleme in NP und NPNP, und erfreut sich mittlerweile zunehmender Beliebtheit, dank ausgereifter Tool-Unterstützung.
Wir verwenden ASP weitestgehend anwendungsorientiert. So zum Beispiel, um unterschiedliche Semantiken für Argumentation Frameworks abzubilden und mit Hilfe von ASP-Solvern effizient zu berechnen.
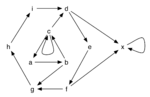
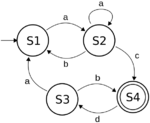
Automatentheorie befasst sich mit der Untersuchung von abstrakten Maschinen, ihren Berechnungen und Berechnungsproblemen. Im Wesentlichen können Automaten als endliche Repräsentationen von (potenziell) unendlichen formalen Sprachen verstanden werden, und sie variieren in ihrer Ausdrucksstärke je nach ihrem spezifischen Design.
Endliche Automaten, die die regulären Sprachen erkennen, sind einer der grundlegendsten Formalismen in der theoretischen Informatik und haben sich in vielen Bereichen als nützliches Werkzeug erwiesen, z. B. beim Bau von Compilern, bei der formalen Verifikation oder als Mittel zum Nachweis der Entscheidbarkeit von ausdrucksstarken Logiken, die zur Wissensrepräsentation eingesetzt werden.
Insbesondere in den genannten Bereichen ist es wünschenswert, Sachverhalte zu modellieren, die über Regularität hinausgehen. In diesem Forschungsprojekt sind wir an (Baum-)Automatenmodellen interessiert, die durch Zählmechanismen erweitert werden.
Beschreibungslogiken sind eines der Hauptparadigmen der Wissensrepräsentation. Sie sind aus semantischen Netzwerken und Frame-basierten Ansätzen entstanden.
Die Beweistheorie beschäftigt sich mit den formalen Eigenschaften und Anwendungsmöglichkeiten mathematischer Beweise. Damit dient sie als eine der tragenden Säulen der mathematischen Logik. Typischerweise werden Beweise als syntaktische Objekte definiert, die induktiv durch Anwendungen von Inferenzregeln auf eine Menge von Annahmen, Axiomen oder im Vorfeld geführten Beweisen, konstruiert werden können. Da Beweise durch das Manipulieren von Formeln und Symbolen durch Inferenzregeln konstruiert werden, ist die Beweistheorie ihrem Wesen nach syntaktisch. Daher sind Beweiskalküle für logisches Schließen im Bereich der Informatik bestens geeignet. In diesem Kontext hat sich die Beweistheorie als effektives Werkzeug im automated reasoning herausgestellt, das es erlaubt, Entscheidungsverfahren zu entwickeln, welche optimal hinsichtlich ihrer Komplexitätseigenschaften sind und sogenannte verifiable witnesses für (un)erfüllbare logische Aussagen bereitstellen. Auf theoretischer Ebene erlauben es Techniken aus der Beweistheorie beispielsweise die Konsistenz, Entscheidbarkeit oder Interpolierbarkeit von Logiken sowie weitere signifikante Eigenschaften zu zeigen.
Typische Fragestellungen der Beweistheorie sind: Was ist ein mathematischer Beweis? Wie können Beweiskalküle konstruiert werden, sodass sie für automated reasoning geeignet sind? Wie könnte ein Beweiskalkül aufgebaut sein, bei dem alle Beweise analytischer Natur sind (d.h. alle im Beweis verwendeten Informationen sind in der Konklusion des Beweises vorhanden)?
Viele natürliche Berechnungsprobleme lassen sich als Constraint Satisfaction Probleme formulieren: gegeben ist eine endliche Menge von Variablen und eine endliche Menge an Bedingungen (Constraints), gefragt ist, ob es eine Lösung gibt, die allen Bedingungen genügt. Für welche Arten von Constraints lassen sich CSPs effizient lösen, und mit welchen Algorithmen? Für welche CSPs kann es solche Algorithmen nicht geben?
Die Datenbanktheorie beschäftigt sich mit einer Vielzahl von Themen im Bereich des Datenbankmanagement und der Datenbankmanagementsysteme. Ihr theoretisches Fundament stammt aus der Logik, insbesondere aus der Relationalen Algebra und der Prädikatenlogik 1. Stufe. Der Fokus liegt unter anderem auf den Komplexitätseigenschaften und der Ausdrucksstärke von Anfragesprachen. Traditionell beschäftigte sich die Datenbanktheorie mit relationalen Modellen, in denen Datenbanken und Anfragen als relationale Strukturen gesehen werden. Das Auswerten einer Anfrage bedeutet in diesem Modell, dass ein passender Homomorphismus zwischen beiden Strukturen gefunden wird. Es lässt sich allerdings beobachten, dass in den letzten Jahren alternative Modelle zunehmend in den Forschungsfokus rücken. Besonders hervorzuheben ist das graphentheoretische Modell, in dem Strukturen auf binäre Signaturen beschränkt und Anfragen zu regulären Ausdrücken erweitert werden.
Existenzielle Regeln sind ein Formalismus zur Wissensrepräsentation mit Anwendungen in der künstlichen Intelligenz und Datenbanken. Ihre syntaktische Allgemeinheit erlauben eine Integration von Formalismen aus der Wissensrepräsentation und aus dem Datenbankbereich. Syntaktisch sind existenzielle Regeln verwandt mit Datalog; ihre wesentliche zusätzliche Ausdrucksstärke besteht in der Möglichkeit, die Existenz von Domänenelementen zu beschreiben, die nicht von vornherein namentlich bekannt sind. Existenzielle Regeln, sind seit längerem unter verschiedenen Bezeichnungen bekannt und die Beantwortung von Anfragen an Daten unter Einbeziehung von existenziellen Regeln ist zur Zeit Gegenstand intensiver Forschung. Typische Fragestellungen hierbei sind beispielsweise: Welche Fragmente existenzieller Regeln verbinden hohe Ausdrucksstärke mit geringer Berechnungsaufwand? Welche allgemeinen Prinzipien garantieren die Entscheidbarkeit der Anfragebeantwortung? Was sind die spezifischen Komplexitäten konkreter Fragmente? Wie entwickelt man effiziente Softwaretools für diese Aufgaben?
Die Formale Begriffsanalyse ist eine mathematische Theorie, welche Begriffe und Begriffshierarchien mit Hilfe der Verbandstheorie beschreibt. Die Grundlage hierbei bilden elementare Datenstrukturen, so genannte formale Kontexte, welche Gegenständen und deren Merkmale beschreiben. Ein formaler Begriff setzt sich dann zusammen aus einer Menge von Gegenständen und einer Menge von Merkmalen, welche der philosophischen und sprachwissenschaftlichen Tradition folgend als Begriffsumfang und Begriffsinhalt bezeichnet werden. Formale Begriffe können dann zueinander in Beziehung gesetzt werden, woraus sich eine Ober-/Unterbegriffs-Hierarchie ergibt. Die Formale Begriffsanalyse wurde in den 1980er Jahren in Darmstadt in der Arbeitsgruppe von Rudolf Wille begründet und hat sich zu einer Disziplin entwickelt welche in vielen Bereichen praktische Anwendung findet, beispielsweise in Data- und Textmining, Wissensmanagement, Semantic Web, Softwareentwicklung, Wirtschaft oder Biologie.
Modal- und Temporallogiken sind logische Formalismen, die auf einer Semantik möglicher Welten basieren. Sie sind dafür geeignet, Phänomene wie das Verhalten von Computerprogrammen, Softwaresysteme, ethische Normen, Wissen und von Agenten ausgeführte Handlungen zu repräsentieren sowie Schlüsse über diese Phänomene zu modellieren. Kanonische Beispiele für solche Logiken sind die grundlegende Modallogik K, die lineare temporale Logik (LTL), Temporallogiken mit verzweigender Zeitstruktur wie CTL oder CTL*, die Dynamische Epistemische Logik sowie STIT-Logiken. Die diesbezügliche Forschung umfasst das präzise Bestimmen der Komplexitätseigenschaften typischer Entscheidungsprobleme und das Entwickeln von effizienten Beweiskalkülen.
Multiagentensysteme (MAS) befassen sich mit der Interaktion autonomer Agenten, die in der Lage sind, unabhängig Entscheidungen zu treffen und in einer gemeinsamen Umgebung agieren. Die MAS-Forschung untersucht, wie Agenten kooperieren, konkurrieren oder ihre Handlungen koordinieren können, um individuelle oder kollektive Ziele zu erreichen. Die theoretischen Grundlagen dieses Feldes stammen aus Disziplinen wie der Spieltheorie, Sozialwahltheorie, verteiltem Rechnen und allgemeiner der Künstlichen Intelligenz. Ein zentrales Anliegen in MAS ist die Gestaltung von Mechanismen, die eine effiziente Zusammenarbeit oder Konkurrenz zwischen den Agenten ermöglichen, insbesondere wenn die Agenten auf der Grundlage klar formulierter Ziele handeln. In unserer Forschung gehen wir häufig davon aus, dass die Agenten mit einer Reihe von möglichen Optionen konfrontiert sind. Obwohl alle Agenten diese Optionen kennen, wissen sie nicht, welche dieser Optionen die richtige oder überlegene Wahl darstellt – die sogenannte „Ground Truth“. In solchen Systemen arbeiten die Agenten zusammen, um diese Ground Truth zu identifizieren, die ihnen zu Beginn noch unbekannt ist.
Die Schlussweise klassischer Logiken (z.B. Prädikatenlogik 1. Stufe) ist monoton, d.h. kann man eine Formel F aus einer Formelmenge M schlussfolgern, so folgt F auch aus jeder Obermenge von M.
Das Nichtmonotone Schließen beschäftigt sich mit Schlussweisen, die diese Monotoniebedingung nicht erfüllen. Dies kann zum Beispiel verwendet werden, um Standard-Annahmen (z.B. „Pakete werden kostenlos versandt, solange nichts anderes angegeben ist.“), Regeln mit Ausnahmen („Vögel können üblicherweise fliegen, Pinguine aber nicht“) oder Prioritäten zwischen Regeln (Bundesgesetze übertrumpfen Landesgesetze) modelliert werden.
Das Forschungsgebiet beschäftigt sich mit der formalen Modellierung nichtmonotoner Schlussweisen, deren Analyse bis hin zu Implementierungen und Anwendungen, z.B. in der Wissensrepräsentation, Logikprogrammierung, juristischem Schließen oder dem Verstehen natürlicher Sprache.
Regelbasiertes Schließen ist das allgemeine Konzept, durch die rekursive Anwendung von Regeln auf Daten neues Wissen zu schließen. Solche Regeln können in verschiedenen Formaten ausgedrückt werden und verschiedene Eigenschaften haben: Datalog Regeln verbieten den Gebrauch von Funktionen und die Einführung neuer existentiell quantifizierter Variablen, letzteres ist mit Existential Rules möglich, andere Logiken wie zum Beispiel Notation3 Logic erlauben die Einführung komplexerer Konstrukte,
Regelbasiertes Schließen kann mit verschiedenen Strategien durchgeführt werden. Beim Forward-Reasoning wendet man sukzessive Regeln auf den gegebenen und abgeleiteten Fakten an, beim Backward-Reasoning geht man rückwärts und beginnt mit einem Ziel, für das man eine gültige Instanz finden möchte. Negation kann entweder so behandelt werden, dass alles, was nicht bewiesen werden kann, als falsch angenommen wird (Negation as Failure) oder die Negation kann eher an die Logik erster Stufe angelehnt sein, wie es bei (Answer Set Programming) der Fall ist.
Diese und andere Aspekte wie zum Beispiel die praktischen Probleme, die durch die verschiedenen Mechanismen gelöst werden können, aber auch die Komplexität der verschiedenen Paradigmen bilden einen Teil unserer Forschung.
Semantische Technologien umfassen eine Vielzahl verschiedener Methoden und Technologien, die der Darstellung, der Verwaltung, dem Austausch oder der Verarbeitung von semantischer Daten dienen. Den Kern dieser Arbeiten bilden maschinen-lesbare Formate für Daten und Schemainformation (Ontologien). Bedeutende Technologiestandards wurden dafür vom World Wide Web Consortium (W3C) verabschiedet, insbesondere im Rahmen der Anstrengungen rund um das sogenannte Semantic Web bzw. Web of Data. Die wichtigsten dieser Standards sind das RDF Resource Description Language (ein graph-basiertes Datenformat), die OWL Web Ontology Language (eine auf Beschreibungslogiken basierende Ontologiesprache) sowie die SPARQL Protocol and RDF Query Language (eine Sprache für Datenbankabfragen und Datenverwaltung). Dennoch umfassen semantische Technologien auch andere Ansätze, wie zum Beispiel die Metadaten-Annotation mittels schema.org, sowie methodologische und infrastrukturelle Aspekte.
Die Forschung im Bereich semantischer Technologien beschäftigt sich mit einer Vielzahl angewandter Fragestellungen. Die Spezifikation und Verarbeitung von Ontologien ist dabei eng mit dem Gebiet der Wissensrepräsentation und des logischen Schließens verwandt, während andere Fragestellungen einen Bezug zu Datenbanken, Informationsextraktion und Web-Systemen haben. Die besondere Natur verteilter Daten im Web spielt besonders im Bereich Linked Open Data eine wichtige Rolle, gleichwohl gibt es viele wichtige Anwendungen von OWL und RDF, in denen das World Wide Web nur eine untergeordnete Rolle spielt.
Das Verstehen natürlicher Sprache befasst sich mit dem Interpretieren und Modellieren der Semantik und Pragmatik von natürlicher Sprache. Dafür werden verschiedenste Techniken angewendet. Da menschliches Schließen oftmals auf der Basis natürlicher Sprache geschieht, ist das Verständnis natürlicher Sprache wichtig für intelligente Systeme, die Menschen beim Schlussfolgern unterstützen sollen. Die für uns relevanten Teilgebiete beinhalten die Repräsentation von und das Schlussfolgern mit Konzepten, wie sie in natürlichen Sprachen vorkomment, z.B. unvollständige Information, unsichere, mehrdeutige oder ungenaue Aussagen, und mit pragmatischer oder nicht-expliziter Information (implizit angenommenem Hintergrundwissen). Die Methoden unserer Ansätze in diesen Gebieten basieren typischerweise (aber nicht ausschließlich) auf der logikbasierten Wissensrepräsentation.
Das Forschungsgebiet Wissensrepräsentation und logisches Schließen befasst sich mit der Darstellung von menschlichem Wissen in Computersystemen und mit der Berechnung logischer Konsequenzen aus diesem Wissen. Durch logische Deduktion leiten solche Systeme implizites Wissen aus den gegebenen Informationen ab. Damit spielt die formale Wissensrepräsentation eine wichtige Rolle zur Konstruktion intelligenter Computersysteme. Aber auch in Anwendungen, in denen große Wissensbasen erstellt werden, werden diese Technologien eingesetzt, da logisches Schließen helfen kann, Redundanz zu vermeiden und Fehler zu entdecken.
Die meisten modernen Ansätze in der Wissensrepräsentation beruhen auf formaler Logik, wobei Beschreibungslogiken und regelbasierte Formalismen die wichtigsten Sprachfamilien darstellen. In vielen Anwendungen sind Wissensbasen die Grundlage für Ontologien, so dass Wissensrepräsentation in enger Beziehung zu anderen Forschungegebieten steht, zum Beispiel zu semantischen Technologien. Obwohl das Grundgerüst der Wissensrepräsentation die theoeretische Forschung auf der formalen Logik ist, umfasst die Forschung in diesem Gebiet auch viele angewandte Fragestellungen, so z.B. die Entwicklung effizienter Tools zum automatischen Schließen.
